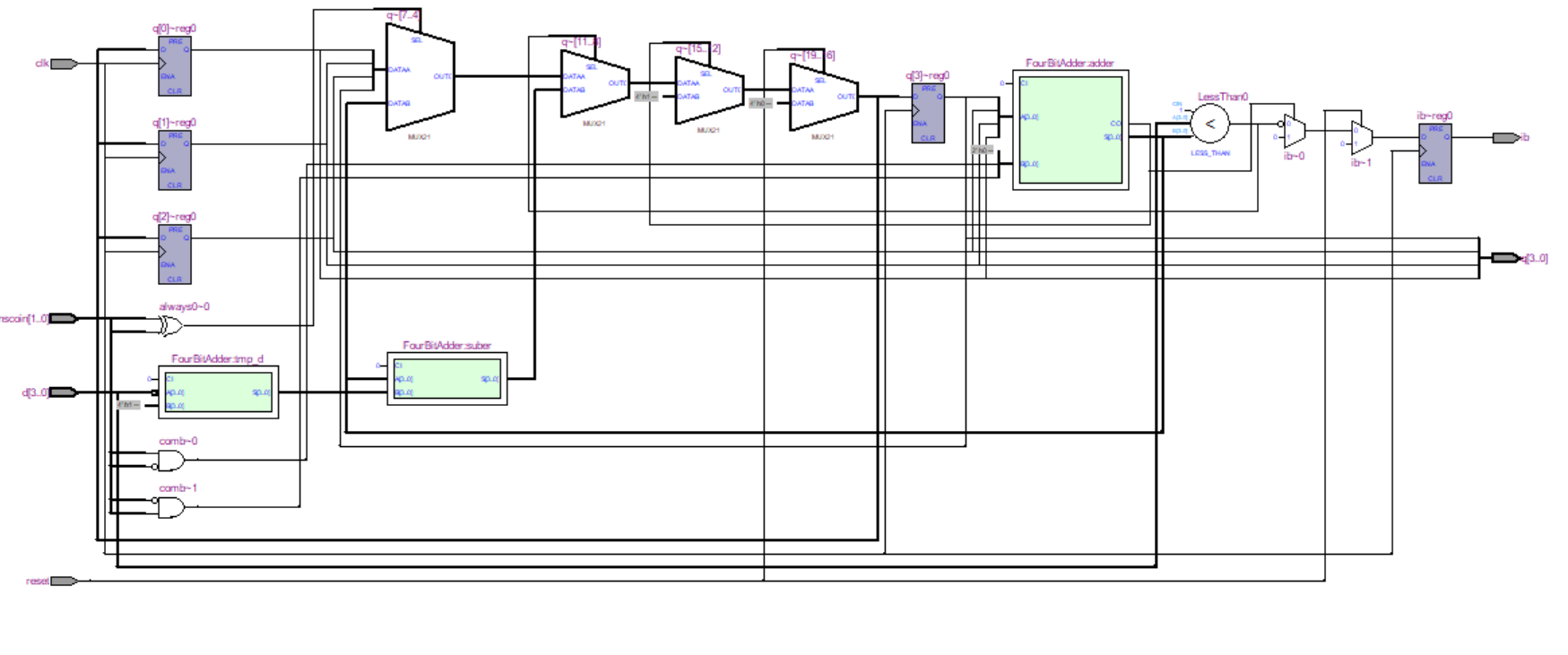
模拟自动售货机(加法器)
题目内容
模拟自动售货机(加法器)
输入信号:投币信号inscoin[1:0]、商品价格信号d[3:0]、时钟信号clk
输出信号:余额信号q[3:0]、余额不足信号ib
设计要求:
1、以0.5元作为一个基本计价单位,商品价格和余额均为整数。
2、初始时,投币信号inscoin[1:0]值为2’b00(即二进制00B),商品价格信号d[3:0]值为4’b0000(即二进制0000B),余额信号q[3:0]值为4’b0000,余额不足信号ib为低电平。
3、投币信号inscoin[0]为高电平表示投入一个0.5元硬币,inscoin[1]为高电平表示投入一个1元硬币,inscoin[1]和inscoin[0]同时为低电平表示未投币,inscoin[1]和inscoin[0]同时为高电平则表示投币无效。
4、时钟信号clk有效时(可选用时钟脉冲的上升沿或者下降沿),余额先加上投币额,再试减去商品价格,如果余额足够,最终减去商品价格得到新的余额,余额不足信号为低电平,如果余额不足,则不减商品价格,余额不足信号为高电平。
硬件设计
根据要求,可以先通过软件思维设计出来:
module auto_machine(
input [1:0] inscoin,
input [3:0] d,
input clk,
input reset,
output reg [3:0] q,
output reg ib);
always @(posedge clk) begin
//额外添加了重置信号(可选)
if(reset) begin
q = 4'b0;
ib = 1'b0;
end else begin
//先判断投币信号,根据信号对余额进行修改
case(inscoin)
2'b01: q = q + 1; // 0.5
2'b10: q = q + 2; // 1
default q = q;
endcase
//对余额处理完后紧接着检测硬币数量是否充足,若充足则扣款
if(q >= d) begin
q = q - d;
ib = 0;
end else begin
ib = 1;
end
end
end
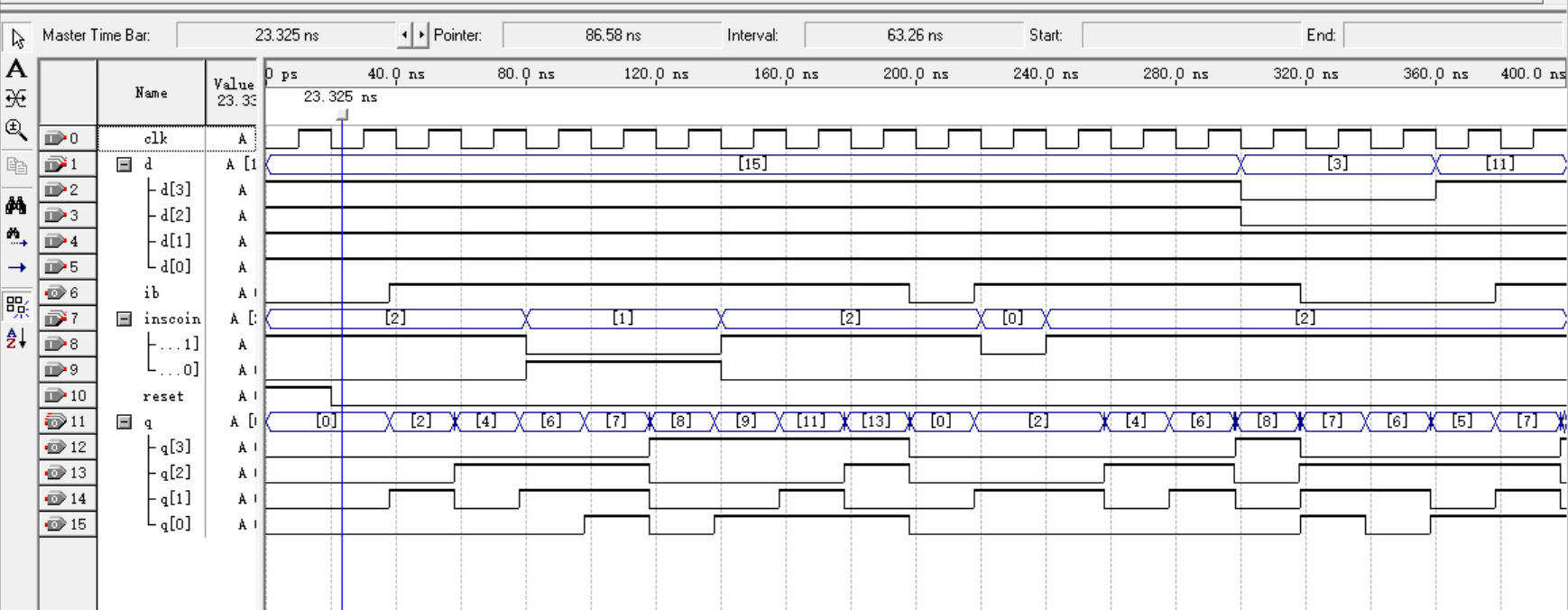
endmodule利用软件思维设计这道题很简单,波形图结果如下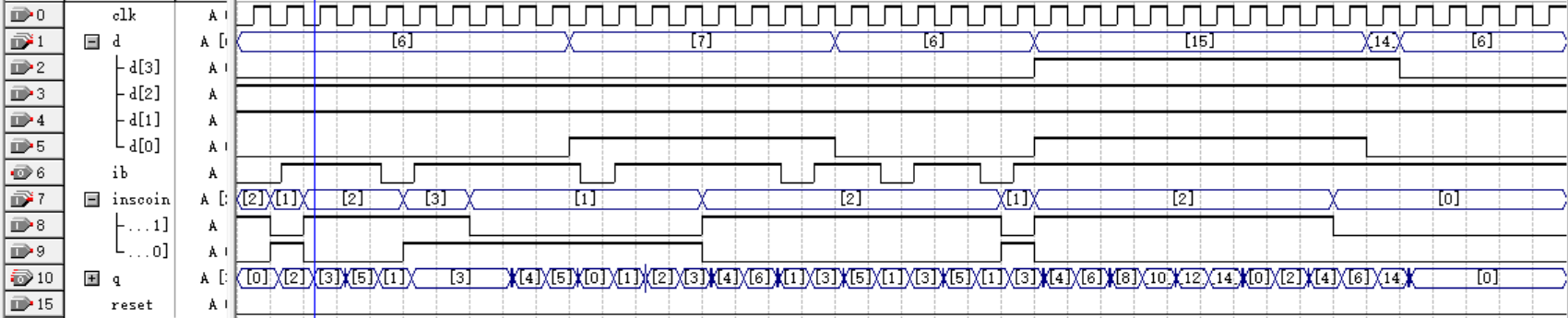
基本没有问题,但注意到,因为我们以0.5元作为基本单位,当商品价格为15个单位,而我们手里的余额为14个单位且下一次投币2个单位时,会导致余额先变为(14 + 2)% 16 = 0,
再去检测就会发现余额不足,因此我们需要解决这种情况
方法很简单,将余额扩充至5位就可以了:
module auto_machine (
input [1:0] inscoin, // 投币输入:01=0.5元, 10=1元
input [3:0] d, // 商品价格(0~15)
input clk, // 时钟
input reset, // 异步复位
output reg [4:0] q, // 当前余额(0~31)
output reg ib // 出货标志:0=可出货,1=余额不足
);
always @(posedge clk) begin
if (reset) begin
// 复位初始化
q = 5'b0;
ib = 1'b0;
end else begin
// 投币逻辑
case (inscoin)
2'b01 : q = q + 1; // 投币0.5元
2'b10 : q = q + 2; // 投币1元
default : q = q; // 无有效投币
endcase
// 扣款判断
if (q >= d) begin
q = q - d; // 扣款
ib = 1'b0; // 允许出货
end else begin
ib = 1'b1; // 余额不足
end
end
end
endmodule
效果图:
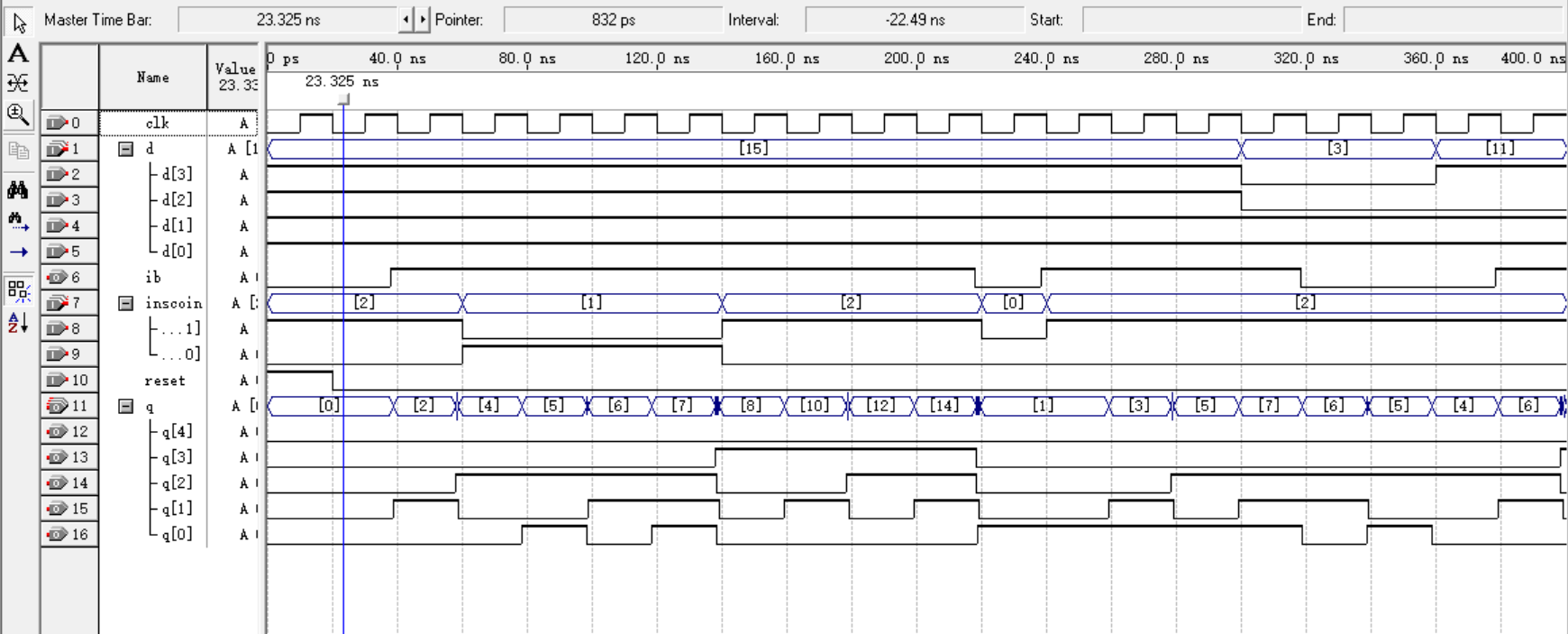
当然,这种软件思维设计逻辑结构会非常复杂:
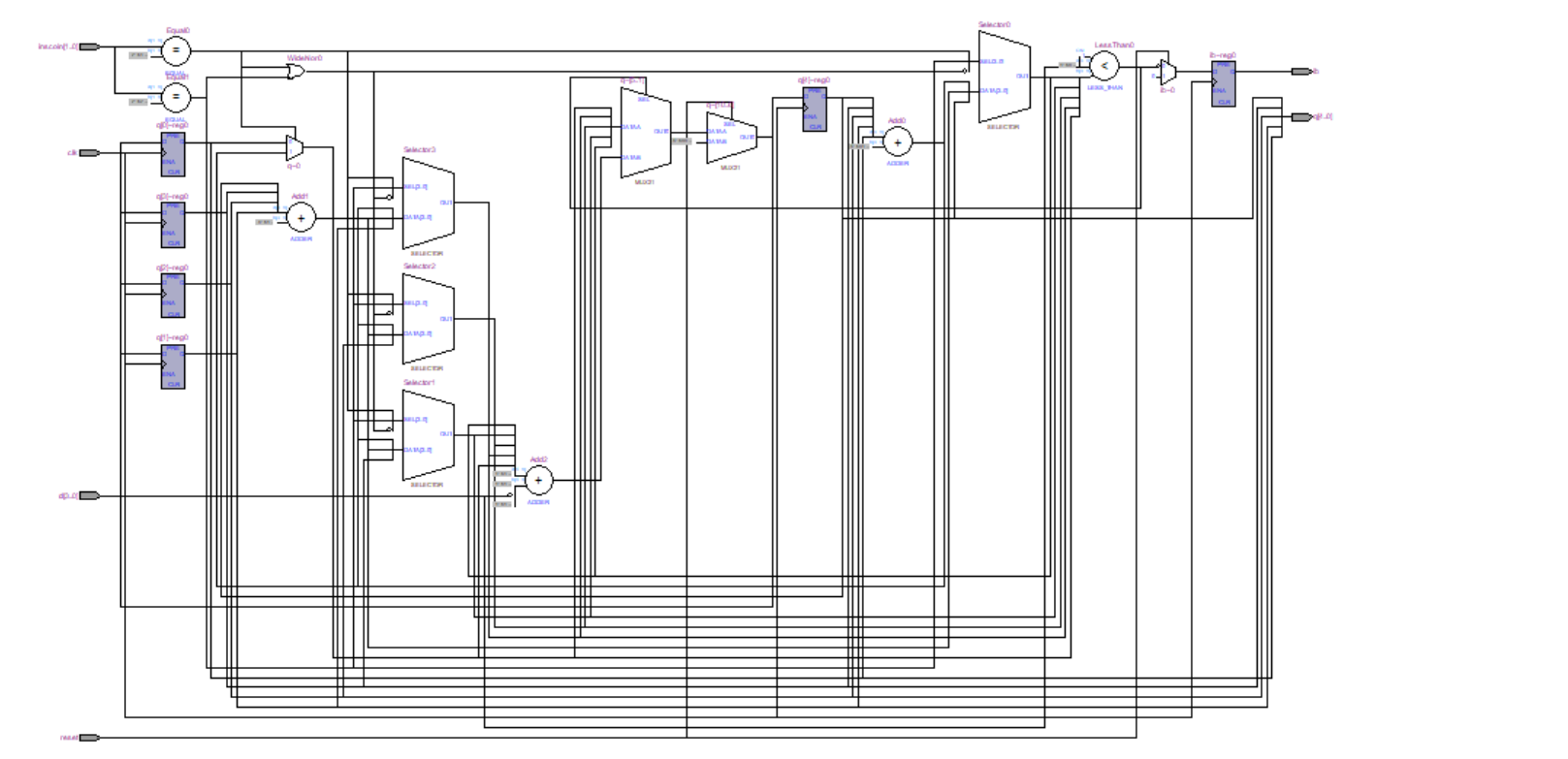
所以我们需要基于这一问题设计一个硬件思维的逻辑结构:
首先实现一个四位加法器替换加法运算:
module FourBitAdder(
input [3:0] A, B,
input CI,
output [3:0] S,
output CO
);
wire [3:0] P = A ^ B;
wire [3:0] G = A & B;
wire [3:0] C;
assign C[0] = CI;
assign C[1] = G[0] | (P[0] & CI);
assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & CI);
assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & CI);
assign CO = G[3] | P[3] & C[3];
assign S = P ^ C;
endmodule该加法器使用的是3位并联加一位串联,在唐朔飞的《计算机组成原理》第285面的6.23中可以看到实现原理,这里不再赘述,但我加了一个小改动,因为串联电路CO若也通过并联方式
来实现的话,那么对于CO而言电路就非常复杂了,实现代码如下:
assign CO = G[3] | P[3] & G[2] | (P[3] & P[2] & G[1]) | (P[3] & P[2] & P[1] & G[0]) | (P[3] & P[2] & P[1] & P[0] & CI);会使用相当多的门电路,所以我单独把 CO 设置成了串联电路,即在 C[3] 计算出来后再利用 C[3] 计算 CO,不过经过测试,直接使用书上的格式效率差不多,所谓力大砖飞
加法器中加的这个数是根据inscoin来判断的,判断如下:
inscoin 输入对应加数 B 映射表
inscoin (二进制) |
投币类型 | B[3:0] (二进制) |
B (十进制) |
实际加钱金额 | 计算逻辑说明 |
|---|---|---|---|---|---|
00 |
无效投币 | 0000 |
0 | +0 元 | B = {2'b00, 0&~0, 0&~0} |
01 |
投币0.5元 | 0001 |
1 | +0.5 元 | B = {2'b00, 0&~1, 1&~0} |
10 |
投币1元 | 0010 |
2 | +1 元 | B = {2'b00, 1&~0, 0&~1} |
11 |
无效投币 | 0000 |
0 | +0 元 | B = {2'b00, 1&~1, 1&~1} |
计算公式
wire [3:0] B = {2'b00, inscoin[1] & ~inscoin[0], inscoin[0] & ~inscoin[1]};计算过程如下:
首先01和10两种情况加上的数就是0001和0010,因此这两种情况直接将 inscoin 的两位数作为最低数即可,而当遇到 inscoin 为00或11时加上得数应当为0,
因此,在 inscoin 两位异或为1时加数是有效的,否则为0,故:
B[1] = inscoin[1] & (inscoin[0] ^ inscoin[1]) = inscoins[1] & ~inscoin[0] (化简过程自己脑补)
B[0] = inscoin[0] & (inscoin[1] ^ inscoin[0]) = inscoins[0] & ~inscoin[1] (你知道我要说什么的)
还有一种方法,利用真值表,可以看到01时低位为1,10时高位为1,所以可以直接拼接出线路来,利用真值表更简单易懂
其次是溢出判断,显然,若出现溢出,一定是因为遇到了14+2的情况(15+1不可能,因为商品价格最高也就是15)此时的商品价格也就是15,因此这种情况特判直接将余额改为1
即可(14+2-15)
优化后代码如下:
module auto_machine (
input [1:0] inscoin, // 投币:01=0.5元, 10=1元
input [3:0] d, // 商品价格(0~15,单位0.5元)
input clk, // 时钟
input reset, // 复位
output reg [3:0] q, // 余额(0~15,单位0.5元)
output reg ib // 余额不足标志
);
wire [3:0] B = {2'b00, inscoin[1] & ~inscoin[0], inscoin[0] & ~inscoin[1]};
// 实例化加法器
wire [3:0] add_result;
wire carry_out;
FourBitAdder adder (
.A(q),
.B(B),
.CI(1'b0),
.S(add_result),
.CO(carry_out)
);
always @(posedge clk) begin
if (reset) begin
q <= 4'b0000;
ib <= 1'b0;
end else begin
// 处理溢出特例
if (carry_out) begin
q <= 1; // 16 - 15 = 1
ib <= 1'b0;
end
// 正常情况(无溢出)
else begin
// 先更新余额(仅当投币有效时)
if (inscoin[1] ^ inscoin[0]) begin // inscoin=01或10
q <= add_result;
end
// 扣款判断
if (add_result >= d) begin
q <= add_result - d;
ib <= 1'b0;
end else begin
ib <= 1'b1;
end
end
end
end
endmodule
module FourBitAdder(
input [3:0] A, B,
input CI,
output [3:0] S,
output CO
);
wire [3:0] P = A ^ B;
wire [3:0] G = A & B;
wire [3:0] C;
assign C[0] = CI;
assign C[1] = G[0] | (P[0] & CI);
assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & CI);
assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & CI);
assign CO = G[3] | (P[3] & C[3]);
assign S = P ^ C;
endmodule再将减法操作改进为加法器实现,这里可以直接复用加法器实现减法器:
module FourBitAdder(
input [3:0] A, B,
input SubEn,
output [3:0] S,
output CO
);
wire CI = SubEn;
wire [3:0] last_B = {4{SubEn}} ^ B;
wire [3:0] P = last_B ^ A;
wire [3:0] G = A & last_B;
wire [3:0] C;
assign C[0] = CI;
assign C[1] = G[0] | (P[0] & CI);
assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & CI);
assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & CI);
assign CO = SubEn ^ (G[3] | (P[3] & C[3]));
assign S = P ^ C;
endmodule
添加一个SubEn选项,用来决定做加法运算还是减法运算,而我们将SubEn利用 {} 符号作位扩展成4bit,然后分别与 B 异或,这样,减数相当于就会在 SubEn 为1的时候被取反(1异或任何数相当于取反),但是补码还要加一怎么办,很简单,给 CI 赋值 SubEn,这样 CI 就会在减法时变成1,相当于加一了,这样就将加减法综合成了一个芯片。
为什么最后的 CO 需要与 SubEn 异或呢?道理很简单:
设被减数是 a, 减数是 b,那么 a - b = a + (~b + 1) = a + (16 - b) = a + 16 - b; 若 CO 位为1,说明a + 16 - b 溢出,也就说明a - b > 0 => a > b
所以如果 CO 为1说明不需要借位,我们需要让 CO 表示是否需要借位,因此在减法运算的时候需要给 CO 取反,也就是将 SubEn 与 CO 异或
这样一来,比较器当然也可以优化掉,针对以下代码,我们可以根据减法的 CO 来判断减数是否比被减数大,若 CO 位为0,则说明被减数比减数大,此时可以售卖商品
因此,减法器的borrow_in对我们而言就至关重要,我们叫他is_enough,用于判断用户钱带没带够,将 if 判断中的 add_result >= d 修改为 is_enough 即可,最终代码如下:
module auto_machine (
input [1:0] inscoin,
input [3:0] d,
input clk,
input reset,
output reg [3:0] q,
output reg ib
);
wire [3:0] B = {2'b00, inscoin[1] & ~inscoin[0], inscoin[0] & ~inscoin[1]};
wire [3:0] add_result, sub_result, comp_d;
wire carry_out, is_enough, unuseful_co;
FourBitAdder adder (
.A(q),
.B(B),
.SubEn(1'b0),
.S(add_result),
.CO(carry_out)
);
FourBitAdder suber (
.A(add_result),
.B(d),
.SubEn(1'b1),
.S(sub_result),
.CO(is_enough)
);
always @(posedge clk) begin
if (reset) begin
q <= 4'b0000;
ib <= 1'b0;
end else begin
if (carry_out) begin
q <= 1;
ib <= 1'b0;
end
else begin
if (inscoin[1] ^ inscoin[0]) begin
q <= add_result;
end
if (~is_enough) begin
q <= sub_result;
ib <= 1'b0;
end else begin
ib <= 1'b1;
end
end
end
end
endmodule
module FourBitAdder(
input [3:0] A, B,
input SubEn,
output [3:0] S,
output CO
);
wire CI = SubEn;
wire [3:0] last_B = {4{SubEn}} ^ B;
wire [3:0] P = last_B ^ A;
wire [3:0] G = A & last_B;
wire [3:0] C;
assign C[0] = CI;
assign C[1] = G[0] | (P[0] & CI);
assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & CI);
assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & CI);
assign CO = SubEn ^ (G[3] | (P[3] & C[3]));
assign S = P ^ C;
endmodule这样就完全规避了加法器,减法器以及比较器,最小化了硬件开销,条件判断开销并不大(均为二路选择器),因此不做优化,测试后没有问题:
结构图优化后如下: